光子を動かす波は関数として求めることができます

　光子は波によってTerminalへと導かれます。この波を関数として求めます。光子は Terminal から情報 Zを受取り、存在できる可能性が高い位置へ移動します。

 　この関数 Z に影響を与える要素(因数といいます)は N しか見つからないので次の2式を検討することから始めましょう。  

      Zs = f(N)　

      Zt = f(-N)  

ここで、Serverの波を Zs とし、Terminal の波を Zt として利用可能な関数が見つかるまで組み合わせを変えていくことにします。

　Server と Terminal の波の点 P の位置のCount を NA.P および NB.P とします。そして、その位置の情報を ZsA.P および ZtB.P とし、点 P が存在できる可能性はZsA.P と ZtB.P の積になると考えると、

       Pst(P)=ZsA.P × ZtB.P = f(NA.P) × f(-NB.P) 　　　　　　　　　　　　　　　　式(2.1-1) 

となります。このPotential Pst(P)の最大値を 1 とします。

　単純な周期関数を図で表すと円周上を動く点の位置とその位置の情報とすることができます。 Nは円周上の一点となり、Z はその点の持つ情報です。

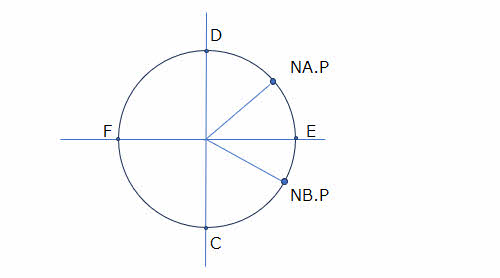
　ZsA.P は光子の情報ですから変化しません。これは円周上の固定点 NA.P の情報です。一方、NB.P はTerminal の Count ですから、その値は変化し円周上を移動します。

図の円周上のどの位置を基準にしてもよいのですが、NA.Pを基準としNB.P がこの位置に来たとき Pst(p)=1 とします。その理由は円周上のこの位置が他と区別できる唯一の固定点だからです。

  求める関数は複素平面上の円になる

 　Pst(P)=1 となるのは NB.P が NA.P の位置にきたときですから、このとき式(2.1-1)を用いて 

       Pst(P) = f(NA.P) × f(-NB.P) = f(NA.P) × f(-NA.P) = 1 　　　　　 式 (2.1-2)  

図の円周上において因数 N が C の位置にある時の関数を Zc し、N が D の位置の時の関数を Zd とするとき

　　　Zc = - Zd

です。Zc を f(NA.P) に置き換え、Zd を f(-NA.P) に置き換えると

       f(NA.P) = -f(-NA.P)　　　　　　　　　　　　　　　　　　　式 (2.1-3)

式 (2.1-2)と式 (2.1-3)より 

      f(NA.P) = i または - i  

この条件を満たすのは複素平面上の円周で表示される複素周期関数になります。

　このような関数はたくさんありますが、とりあえず単純な次の式を用います。

w は常数です。

　　ZA.P = exp(iw × NA.P) 　　　　　　　　　　　　　　　　　式 (2.1-4)

        ZB.P = exp(-iw × NB.P) 　　　　　　　　　　　　　　　　　式 (2.1-5)

　　Pst(P) = exp(iw × (NA.P - NB.P)) 　　　　　　　　　　　　　式 (2.1-6)

　この関数は NA.P - NB.P =0 のとき Pst(P) = 1 であり、NA と NB は同時にその Count を 1 ずつ増やしていくので Pst(P) = 1 が継続されます。

別の見方をすると、点 P が移動するときは図の円周上でNB.P が  NA.P の上にある時ですから

　 NA.P - NB.P = 0

となり 、光子はこの波を示す式(2.1-6)によって進む事になります。

修正記録

 　2024-01-03: 理解し易いように文章の一部を修正しました。